La lumière a toujours constitué pour moi un phénomène fascinant. Elle façonne notre perception du monde en révélant ses couleurs, ses formes, et sa profondeur. Pourtant, malgré son omniprésence dans notre vie, la véritable nature de la lumière a longtemps échappé aux scientifiques et philosophes. Ce n’est qu’à partir du 19ᵉ siècle, avec les travaux révolutionnaires de chercheurs tels que Thomas Young et James Clerk Maxwell, et au 20ᵉ siècle avec ceux de Max Planck, Albert Einstein et d’autres pionniers, que nous avons vraiment commencé à comprendre les  propriétés fascinantes de la lumière.

Les premières tentatives pour expliquer ce phénomène remontent au XVIIᵉ siècle où le grand Isaac Newton fut l’un des premiers à proposer une théorie, selon laquelle la lumière était composée de petites particules ou « corpuscules » se déplaçant en ligne droite. Ce modèle permettait d’expliquer la réflexion de la lumière, lorsque ces corpuscules rebondissaient sur les surfaces réfléchissantes.
À la même époque, un autre scientifique de renom, Christiaan Huygens, offrait une vision radicalement différente. Il suggérait que la lumière n’était pas composée de particules, mais d’ondes. Il comparait ce phénomène à une vague qui traverse l’océan, déformant la surface de l’eau en se propageant. Huygens proposa qu’un support invisible et hypothétique, appelé l’éther, permettait à la lumière de se propager à travers l’univers comme une onde.
Ces deux théories, celle de Newton sur la nature corpusculaire de la lumière et celle de Huygens sur sa nature ondulatoire, ont posé les bases des recherches scientifiques qui ont suivi. Des décennies plus tard, de nouvelles découvertes allaient venir enrichir et complexifier notre compréhension de ce phénomène.

Dans cet article, nous allons explorer  l’hypothèse de la nature ondulatoire de la lumière en étudiant la célèbre expérience de la double fente de Young. Nous allons aussi tenter de comprendre la nature fondamentale de la lumière en faisant parler les équations de Maxwell.

L’expérience de la double fente de Young :

Pourquoi la lumière serait-elle une onde ? D’un premier abord, il s’agit là d’une hypothèse pas si facile à vérifier. Et comme pour toute théorie en physique, il est nécessaire de réaliser des expériences pour l’affirmer ou l’infirmer. Une des expériences les plus importante de toute la physique moderne est la célèbre expérience de la double fente de Young.  Le principe est simple : Il s’agit de placer une source lumineuse derrière 2 fentes et d’observer sur un écran placé de l’autre coté la figure qui en résulte (voir fig ci-dessous).

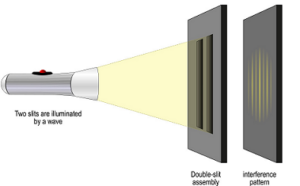
Dans notre cas, on observe ce que l’on appelle des « Franges d’interférences » c’est-à-dire une figure alternée de tâches sombre et de tâches lumineuses.  Si la lumière était composée de petites particules (corpuscules) comme le suggérait newton, nous aurions obtenu 2 traits sur l’écran (Soit la particule passait par la fente 1, soit la particule passait par la fente 2, soit elle était bloquée).

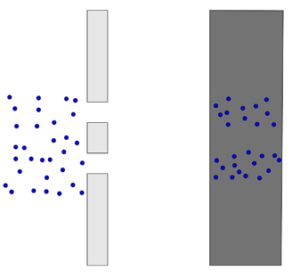
La figure ci-dessus montre le cas d’une expérience faite avec de petites billes et où l’on voit se former 2 tâches sur l’écran d’arriver. Or dans notre expérience, on obtient une alternance de franges lumineuses et sombres. Comment peut-on expliquer ce phénomène ?

Explication qualitative :

Les franges d’interférence sont une signature claire du comportement ondulatoire de la lumière. En effet, lorsqu’une onde lumineuse traverse les deux fentes, elle se divise en deux sous-ondes qui se propagent vers l’écran. Si la lumière était composée de petites particules, chaque particule passerait soit par la fente 1, soit par la fente 2, produisant deux bandes distinctes sur l’écran. Or, dans cette expérience, les sous-ondes issues des deux fentes interagissent entre elles, et cette interaction crée des zones d’interférences.Lorsque les crêtes des deux ondes lumineuses se superposent, elles s’additionnent et forment des bandes lumineuses : c’est ce qu’on appelle une interférence constructive. À l’inverse, lorsque la crête d’une onde coïncide avec le creux d’une autre, elles s’annulent, créant ainsi des bandes sombres : c’est l’interférence destructive.

Analogie avec les vagues d’eau :

Pour mieux comprendre cette idée, on peut faire une analogie avec les vagues à la surface de l’eau. Imaginons que l’on crée des vagues régulières dans une bassine, et que ces vagues passent à travers deux ouvertures. De la même manière que pour la lumière, les deux séries de vagues se croisent et interagissent entre elles. Aux endroits où les vagues s’additionnent (interférence constructive), on observe des vagues plus hautes, et aux endroits où elles s’annulent (interférence destructive), la surface de l’eau est plus calme. Sur un écran, cela se traduirait par une alternance de bandes correspondant à des vagues hautes et basses, de manière très similaire à ce que l’on observe avec la lumière dans l’expérience de Young.

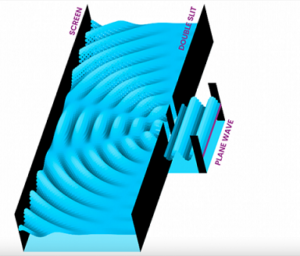
L’expérience de la double fente de Young a donc permis de démontrer de manière claire et intuitive que la lumière se comporte comme une onde. Ce résultat a été une percée majeure, car il contredisait la vision corpusculaire de Newton, qui dominait à l’époque. Bien sûr, en physique, les intuitions et les analogies ne suffisent pas : pour confirmer ces résultats, il a fallu les mettre en équation et développer des théories capables de rendre compte de ces observations de manière quantitative. Et c’est ce que nous allons développer dans la suite de cet article.

Comment modéliser mathématiquement un onde ?

À partir de ce qui a été discuté précédemment, on comprend que la lumière se comporte comme une onde. Mais comment pouvons-nous modéliser mathématiquement une onde ? Pour cela, nous avons besoin d’une fonction mathématique qui représente un phénomène périodique. On peut par exemple choisir la fonction cosinus pour faire notre construction. En effet, la fonction $ cos(x) $ peut décrire une onde plane où chaque point de l’espace $ x $ est associé à une valeur de l’onde comprise entre 1 et -1. Cette fonction oscille de façon régulière, capturant l’aspect cyclique d’une onde.
Cependant, cette forme basique ne suffit pas pour modéliser toutes les ondes planes, car une onde peut avoir une amplitude plus ou moins grande. C’est-à-dire que les pics de l’onde peuvent dépasser la valeur de 1. Pour cela, nous introduisons un facteur $ A $ appelé amplitude de l’onde, qui représente la hauteur maximale des oscillations de l’onde. La forme de l’onde devient alors : $ A cos(x) $ . Ce facteur $ A $ permet de modéliser l’intensité de l’onde, que ce soit la hauteur des vaguelettes dans l’eau ou l’intensité lumineuse dans le cas de la lumière.

Pour aller plus loin, il faut aussi prendre en compte la distance entre les différents pics de l’onde. Cette distance est appelée la longueur d’onde $ \lambda $ . Une onde avec des pics rapprochés a une longueur d’onde courte, tandis qu’une onde avec des pics éloignés a une longueur d’onde longue. On introduit donc un facteur $ k $ appelé le nombre d’onde, pour ajuster cette distance entre les pics dans notre modèle. La forme de notre onde devient alors : $ A cos(k.x) $ et on montre trivialement que le nombre d’onde est relié à la longueur d’onde par l’expression : $ k = \frac{2\pi}{\lambda} $ .
Cela signifie que plus $k$ est grand, plus les pics de l’onde sont rapprochés, ce qui correspond à une longueur d’onde plus courte.

Jusqu’ici, notre modèle décrit une onde qui est statique, c’est-à-dire qu’elle ne se déplace pas. Or, dans la réalité, les ondes, qu’elles soient lumineuses, sonores, ou de l’eau, se déplacent. Pour prendre en compte ce déplacement, il est nécessaire d’introduire un facteur temps $ t $ . Ainsi, l’onde évolue dans le temps et peut se propager le long d’un axe. On modifie l’expression de notre onde pour qu’elle devienne : $ A cos(kx – \omega  t)$ . Ici, $\omega$ est la pulsation angulaire (ou fréquence angulaire), qui représente la vitesse à laquelle l’onde oscille dans le temps. Le signe – signifie que l’onde se déplace vers la droite ; si le signe était +, l’onde se déplacerait vers la gauche.
Enfin, il est parfois nécessaire de prendre en compte la phase initiale de l’onde. La phase notée $ \phi_0 $ permet de spécifier la position de l’onde au temps $ t=0 $ et à la position $ x=0 $ . Par exemple, si l’onde commence à un point différent dans son cycle, il faut ajuster cette valeur pour correspondre à la réalité observée. L’expression finale d’une onde plane devient donc :

$ \boxed{ A cos(kx-\omega t+ \phi_0)} $

La figure ci-dessous permet de visualiser les différents paramètres que l’on a modéliser au sein de notre expréssion d’onde plane :

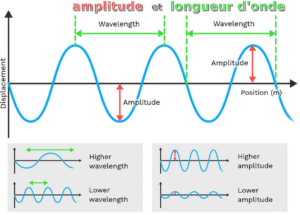
En résumé, pour modéliser une onde, nous avons besoin de trois éléments fondamentaux : l’amplitude $A$ , qui détermine l’intensité de l’onde ; le nombre d’onde $k$ qui définit la distance entre les pics de l’onde ; et la pulsation $\omega$ qui décrit la vitesse à laquelle l’onde oscille dans le temps. Ces éléments, combinés avec un éventuel facteur de phase $\phi_0$ nous permettent de construire un modèle mathématique complet qui correspond aux observations expérimentales.

Explication théorique de l’expérience de Young :

Maintenant que nous avons vu comment modéliser une onde plane, nous pouvons tenter d’expliquer les franges d’interférence observées sur l’écran dans l’expérience de Young. Ces franges, qui alternent entre des bandes lumineuses et sombres, sont la conséquence directe du caractère ondulatoire de la lumière et des interférences entre les deux ondes issues des deux fentes.

La différence de marche :

Pour modéliser ce phénomène, considérons un point $P$ sur l’écran, et appelons $r_1$ et $r_2$ les distances séparant ce point des deux fentes. La différence entre ces deux distances est appelée différence de marche $(\delta) =r_2 – r_1 $  . Cette différence de marche est cruciale, car elle détermine le déphasage entre les deux ondes lorsqu’elles atteignent le point $P$.

$A$

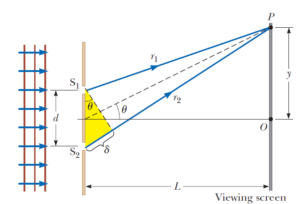
Superpostion des ondes sur l’écran

L’onde on provenance de la première fente s’exprime comme suit : $E_1 = E_0 cos(kx – \omega t) $ ; l’onde en provenance de la fente 2 a la même forme que l’onde 1 sauf qu’elle est décalée à cause de la différence de marche, son expression est donc : $E_1 = E_0 cos(k(x+\delta) – \omega t) $ . L’onde résutlante sur l’écran est donc la somme de ces 2 ondes : $E_1 = E_0 cos(kx – \omega t) + E_0 cos(k(x+\delta) – \omega t) $ que l’on peut simplifier en utilisant l’identité suivante : $ cos A + cos B = 2 cos ( (A+B)/2) cos ((A-B)/2)$. Nous obtenons donc l’expression de l’onde superposée :

$ \boxed{ 2 E_0 cos(\frac{k \delta}{2}) cos(kx-\omega t + \frac{k \delta}{2}) } $

Intéprétation physique : 

L’intensité lumineuse perçue par l’œil humain est proportionnelle au carré du module de l’onde. Cela signifie que lorsque deux ondes lumineuses se superposent, l’intensité que nous observons dépend directement de la manière dont les amplitudes des ondes interfèrent entre elles. Les maximums de l’onde résultante correspondent à des zones d’interférence constructive, que l’on observe sous forme de franges lumineuses. Inversement, les minimums correspondent à des zones d’interférence destructive, où les ondes s’annulent partiellement ou totalement, ce qui crée les franges sombres.
Mathématiquement, cela se traduit comme suit :

• Frange lumineuse : $\delta = m \lambda$ 
• Frange sombre : $\delta = (m+\frac{1}{2}) \lambda$ 

Avec un m entier naturel.

On peut même calucler la position des $y$ de chaque frange : $y = L tan(\theta) $ mais puisque $\theta $ est très petit, on peut faire l’approximation : $y = L \theta $ . Or $\theta = \frac{\delta}{d}$ donc :

$y = \frac{L \delta}{d} $

et en remplaçant l’expression de delta pour les franges lumineuses et sombres nous pouvons déduire leurs positions exactes.

Finalement, il apparaît que ces prédictions théoriques concordent parfaitement avec les résultats expérimentaux observés. Les positions des franges lumineuses et sombres, calculées à partir des équations décrivant l’interférence des ondes lumineuses, correspondent exactement aux motifs mesurés sur l’écran dans l’expérience de Young. Cette correspondance entre la théorie et l’observation constitue une validation cruciale du modèle ondulatoire de la lumière.

Echec et Mat pour Isaac Newton ?

Dans un article ultérieur, nous examinerons comment la nature ondulatoire de la lumière est profondément enracinée dans les équations de Maxwell, qui décrivent l’électromagnétisme. Ces équations montrent que les ondes lumineuses sont en réalité des ondes électromagnétiques, une découverte fondamentale qui a révolutionné notre compréhension du phénomène lumineux. Cela semble renforcer l’idée que Newton avait tort en adoptant une approche exclusivement corpusculaire.

Mais Newton a-t-il vraiment perdu cette partie d’échecs ? Pas si sûr ! La nature est en effet bien plus complexe qu’elle ne paraît à première vue. Nous découvrirons, dans d’autres articles, que des physiciens tels qu’Albert Einstein et Arthur Compton ont montré que la lumière possède également un comportement corpusculaire.

Ainsi, nous nous retrouvons face à un mystère fascinant : la lumière est-elle finalement une onde ou une particule ? La réponse à cette question est l’un des fondements de la mécanique quantique, une science révolutionnaire et parfois contre-intuitive, qui défie nos perceptions classiques de la réalité. La lumière ne peut être décrite ni exclusivement comme une onde, ni uniquement comme une particule. Elle possède une dualité onde-particule, un concept fondamental qui sera abordé dans d’autres articles.

En fin de compte, Newton n’a pas réellement perdu la face. Sa vision corpusculaire de la lumière, bien que incomplète, reste partiellement valide dans certaines situations. Le mystère de la lumière continue de défier notre compréhension, et la science, tout comme un jeu d’échecs, est un processus évolutif, où chaque nouvelle découverte nous rapproche un peu plus de la vérité, sans jamais la clore définitivement.